Zhuolin Qu
Modeling malaria immunity
Malaria is one of the deadliest
infectious diseases globally, causing hundreds of
thousands of deaths each year. It disproportionately
affects young children, with two-thirds of fatalities
occurring in under-fives. Individuals acquire protection
from disease through repeated exposure, and this immunity
plays a crucial role in the dynamics of malaria
spread.
Age-structured PDE model: vector-host epidemiological dynamics + immunity dynamics
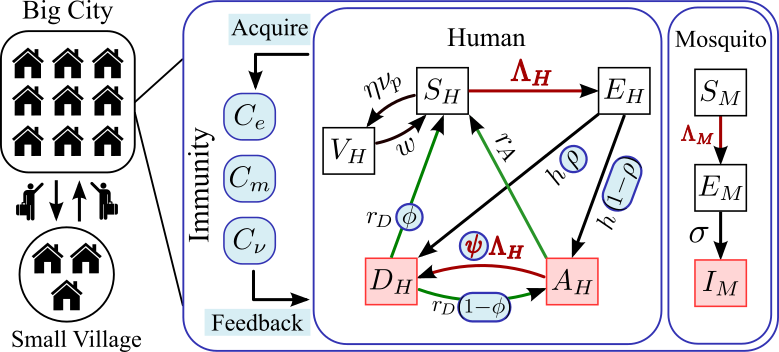
Figure: Schematic of the immuno-epidemiological
model that couples the human-mosquito transmission
dynamics with immunity dynamics. It also captures the
corresponding feedback on the epidemiological parameters
(in blue circles: rho, phi, psi).
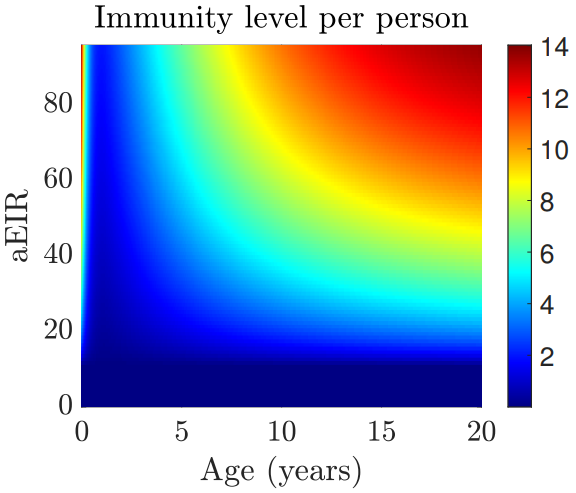
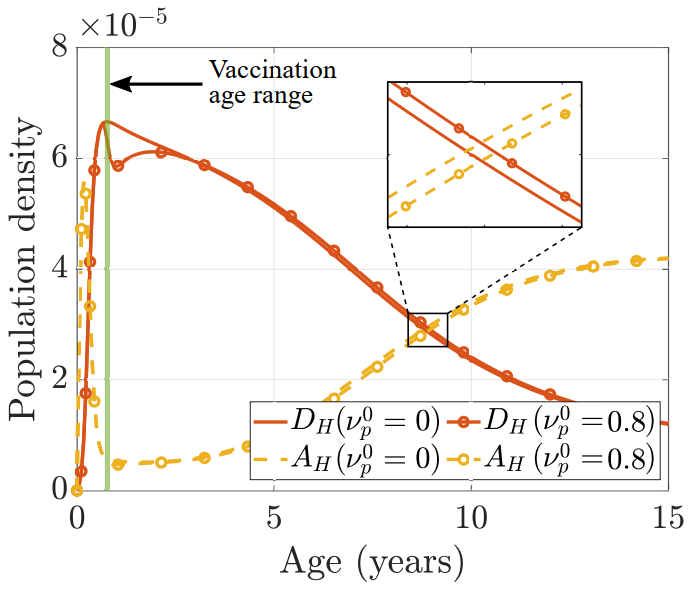
Left: The model characterized the heterogeneity in immunity profiles, which depend on age and malaria transmission level (aEIR) in the region. Right: Preliminary case study of applying RTS,S vaccine in Kenya. Vaccination lowers the severe disease cases before 3 y.o. and slightly increases that number for older ages.
Publication
Zhuolin Qu*, Denis Patterson*, Lauren Childs, Christina
Edholm, Joan Ponce, Olivia Prosper, and Lihong Zhao
Modeling
Immunity
to Malaria with an Age-Structured PDE Framework
*denotes equal contribution
SIAM Journal on Applied Mathematics, 83.3, (2023),
1098-1125.
Collaborators
Lauren Childs,
Virginia Tech
Christina
Edholm, Scripps College
Denis
Patterson, Durham University
Joan Ponce,
Arizona State University
Olivia
Prosper, University of Tennessee, Knoxville
Lihong Zhao,
Virginia Tech